Sums of Random Variables
Sums of Random Variables
Nomenclature:
Upper case letters, \(X, Y\), are random variables; lower case letters, \(x, y\), are specific realizations of them. Upper case \(F\) is a cumulative distribution function, cdf, and lower case \(f\) is a probability density function, pdf.
Sometimes you need to know the distribution of some combination of things. The sum of two incomes, for example, or the difference between demand and capacity. If \(f_X(x)\) is the distribution (probability density function, pdf) of one item, and \(f_Y(y)\) is the distribution of another, what is the distribution of their sum, \(Z = X + Y\) ?
As a simple example consider X and Y to have a uniform distribution on the interval (0, 1). The distribution of their sum is triangular on (0, 2).
Why? To begin consider the problem qualitatively. The minimum possible value of \(Z = X + Y\) is zero when \(x=0\) and \(y=0\), and the maximum possible value is two, when \(x=1\) and \(y=1\). Thus the sum is defined only on the interval \((0, 2)\) since the probability of \(z \lt 0\) or \(z \gt 2\) is zero, that is, \(P(Z \lvert z \gt 0) = 0\) and \(P(Z \vert z \gt 2) = 0\).
Proof:
Further, it seems intuitive(1) that the most probable value would be near \(z=1\), the midpoint of the interval, for several reasons. The summands are iid (independent, identically distributed) and the sum is a linear operation that doesn’t distort symmetry. So we would surmise that the probability density of \(Z = X + Y\) should start at zero at z=0, rise to a maximum at mid-interval, z=1, and then drop symmetrically to zero at the end of the interval, z=2. We might expect the distribution of \(Z = X + Y\) to look like this:
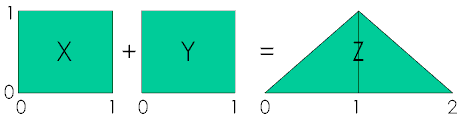
Enough of visceral pseudo calculus. How do you prove that this result is correct?
Note:
- Statistical intuition can sometimes be misleading. See Joseph P. Romano, Andrew F. Siegel (1986) Counterexamples in Probability and Statistics (Wadsworth and Brooks/Cole Statistics/Probability Series)
\(F_Z(z)\), the cdf of \(Z\), is the probability that the sum, \(Z\), is less than or equal to some value \(z\). The probability density that we’re looking for is \(f_Z(z) = d\big( Z(z) \big) /dz\), since the integral of the pdf is the cdf. as a consequence of the Fundamental Theorem of Calculus.
|
1 |
\[F_Z(z)=P(Z \le z)=P(X+Y \le z)\] | by definition. |
|
2 |
\[=\int_{-\infty}^{\infty} P(X+Y \le z \space \lvert \space X=x) \times f_X(x) dx\] | by the definition of conditional probability and the independence of \(X\) and \(Y\) |
|
3 |
\[F_Z(z)=\int_{-\infty}^{\infty}P(x+Y \le z) \times f_X(x) dx\] |
letting \(X = x\) |
|
4 |
Now,
\[P(x+Y \le z) = F_Y(z-x)\] |
by the definition of \(F_Y\) |
|
5 |
so that
\[F_Z(z)=\int_{-\infty}^{\infty} F_Y(z-x) \times f_X(x) dx\] |
by substitution of 4 into 3. |
|
6 |
Also, \[f_Z(x)=\frac{d F_Z(z)}{dz} \] |
by the relationship between a pdf and its cdf. |
|
7 |
\(f_Z(z)= \frac {d}{dz} \Big( \int_{-\infty}^{\infty} F_Y(z-x) \times f_X(x) dx \Big)\) | by substituting 5 into 6. |
|
8 |
\[f_Z(z) = \int_{-\infty}^{\infty} \frac{dF_Y(z-x)}{dx} f_X(x) dx\] |
by Liebnitz’s rule for differentiating an integral. |
|
9 |
Since,
\[f_Y(y) = \frac{dF_Y(y)}{dy} \times \Big(\frac{dy}{dx} = 1 \Big) = \frac{dF_Y(y)}{dz} \] |
by the relationship between a pdf and its cdf and the fact that since \(y = z – x, dy = dz\) |
|
10 |
Finally,
\[f_Z(z) = \int_{-\infty}^{\infty} f_Y(z-x) \space f_X(x) dx \] |
Q.E.D. by substituting 8 into 7 This is a general result. |
|
11 |
\[f_X(x)=1 \text{ and } 0 \le x \le 1\] | Our specific example: Sum of two standard uniform densities. |
|
12 |
and
\[f_Y(y)=1 \text{ and } 0 \le y \le 1\] |
by the definition of a standard uniform distribution |
|
13 |
\[f_Z(z)=\int_{-\infty}^{\infty} 1 \times 1 \space dx\] |
from 10, 11 and 12 above, |
|
14 |
Breaking the integral into to parts depending on \(z\)
\[f_Z(z)=\int_0^x dx=x \lvert_0^1 = z\] |
if \(0 \le z \le 1\), and |
|
15 |
\[f_Z()z)=\int_0^1 dx = x \lvert_{x-1}^1 =1-(z-1) = 2-z\] |
if \(1 \le z \le 2\) |
| Which are seen to be the equations describing a triangular distribution on \((0, 2)\) shown in the figure above. | Q.E.D. |
Note that 10, above, is called the convolution of functions \(f_X(x) \) and \(f_Y(y)\). This result is general and it true for any independent continuous densities. A specific example is our original problem when \(f_X(x) \) and \(f_Y(y)\) are both uniform on \((0, 1)\) and \(Z = X + Y \)is their sum.

