Here’s a great idea:

• Rather than build expensive POD specimens, let’s take the parts inspected at depot and set aside those with indications for use as POD specimens.
• We can identify the size that produced the indication and then “analyze” the data using mh1823 POD methods. (We’ll save tons of money.)

Field-finds are the most detectable cracks in a given size range, since those are the ones your inspection found. It is irresponsible to use these most-detectables to represent all of the cracks because you will grossly over-estimate your inspection’s capability, claiming, for example, 90% POD when the true detectability is closer to 50%.

The statistical properties of Field-Finds are radically different from Probability-of-Detection (POD) demonstration specimens. MIL-HDBK-1823A methods require that you know the entire population of cracks to be inspected. So even if a crack is missed in a POD demonstration, its size and other characteristics are known because it is a laboratory specimen. Special methods (censored regression) can then be used with known misses to determine the \(\hat{a} \textit{ vs a}\) (signal vs. size) relationship, and from that the POD(a) function.

But with field-finds you know what you found, but you don’t know what you missed. So the methods of ordinary regression and censored regression cannot be used because their underlying requirements are not satisfied.  Thus, using MIL-HDBK-1823A methods to analyze field-finds from an unknown population of cracks will grossly over-estimate Probability of Detection for field inspections.  This is illustrated in the following figures.

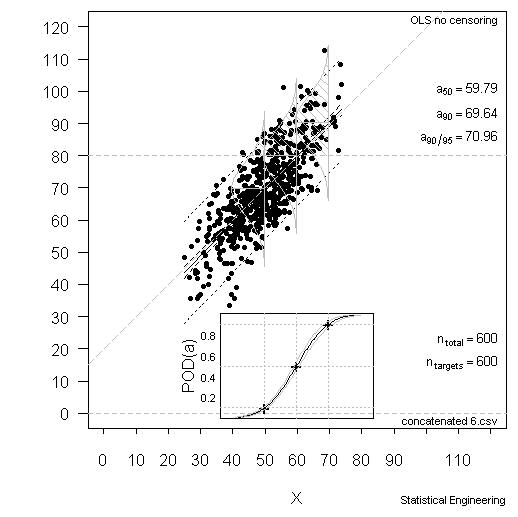
Figure 1 – MIL-HDBK-1823A Methods Work Well with POD Demonstration Specimens

 

The data are 600 simulated observations with the decision threshold set at 80 y-units (\(\hat{a}\)) of which 122 had \(\hat{a}\) values above the threshold of 80.  A MIL-HDBK-1823A analysis produced the results in Figure 1, with these results:

These values are “correct” and are based on all 600 observations.

Now consider the situation where only 122 of the observations were “found.:  (Note, too, that 122 would be considered a “large” sample size.)  All that is known is what is contained in the 122 observations with \(\hat{a}\) above \(\hat{a}_{decision} = 80\), as illustrated in Figure 2.

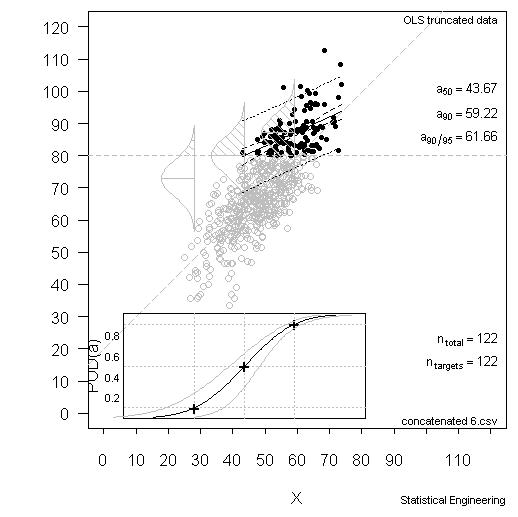
Figure 2 – OSL Regression Methods Over-estimate POD for Field-Finds

 

The data in gray are unknown. Since only the observations above \(\hat{a}\) = 80 are known, they pull the left side of the line sharply upward because the data that would otherwise pull it back into place are not known. Furthermore, since a considerable fraction of the data is missing, the observed \(\hat{a} \textit{ vs a}\) scatter appears much smaller (probability densities in Figure 2) than it really is (Figure 1). The POD based only on the “finds” produces these results:

That is, the a_90/95 capability is optimistically and anti-conservatively too small by 9 size units (62 vs. 71).  This is an enormous overestimation of POD capability.  The POD (at 95% confidence) for a = 62 is not 90% as a naive analysis would suggest, but about POD = 50%, as seen in Figure 1.

In other words we are 95% confident that the inspection will find about half the cracks of size 62 or larger, not 90% of them.  This offers a partial explanation of why inspections whose capability is (erroneously) based on field-finds still experience large misses when inspecting future field-service parts.

There are several things to keep in mind:  The data that are plotted in gray in Figure 2 are unknown to the analysis. They cannot be used, as in Figure 1, because they are known in Figure 1 but unknown in Figure 2.  Furthermore, censored regression can’t work either because the cracks that were not found were not known to have been missed, which is a requirement for censored regression (see MIL-HDBK-1823A, Appendix G “Statistical Analysis of NDE Data”).

The sky is not falling, of course.  Field-finds can be used as NDE specimens but they require special statistical methods to do that.  I can help you and your enterprise analyzed field-finds correctly and avoid dangerous over-estimation of your system’s capabilities.