Some data are “censored.”

That means the response, \(\hat{a}\), is unknown, other than being smaller than some (noise) threshold value, \(\hat{a}_{th}\)
(left-censored) or greater than some saturation limit, \(\hat{a}_{sat}\) (right-censored).  An unknown value that is known to reside in some interval, \(\hat{a}_{min} \le \hat{a}_{th} \le \hat{a}_{max}\) , is interval-censored.

If the censoring value is substituted for the true, but unknown response, an ordinary regression will produce a very skewed result because the line will try to go through the censoring values, rather than the true (but unknown) values.  You can see an example of correct censored regression here, where the data plotted with open symbols are unknown other than being left-censored.

MIL-HDBK-1823A relies on censored regression for continuous-response \(\hat{a} \space \textit{vs} \space a\) data.

Why Ordinary Regression won’t work:

If you don’t know the true value of the response, it’s obvious that you also don’t know how big the error is between the response and the regression line relating the response to the independent variable.  And that means you can’t minimize the summed-squared-errors because you don’t know the errors.  So OLS (Ordinary Least-Squares) can’t work.

(Well, OK, you can get it to work by giving it bogus values for the unknown, censored, observations, but of course your answer will also be bogus.  You can’t fool Mother Nature – even if you can fool yourself.)

You may not use ordinary regression methods with censored data.   You can use them – but your answer will be WRONG.

How Censored Regression works:

The method of least-squares has been quite successful for the more than 200 years since Gauss suggested it, so any new criterion would have to compare favorably with OLS.  R.A. Fisher revolutionized applied statistics early in the 20th century with the idea of likelihood – the probability that the experiment turned out the way that it did.

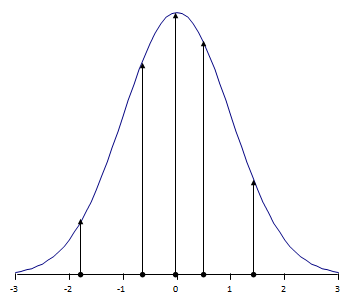
Figure 1: For ordinary observations, likelihood is the ordinate of the probability distribution of the errors.

But when the observation is censored, we don’t know the ordinate.  It could be any ordinate for which â < â_th.  So the likelihood for such left-censored observations is defined to be the area under the probability density between \(-\infty\) and the censoring value, \(\hat{a}_{th}\).

Where OLS methods are applicable, parameter estimates using the maximum likelihood criterion are exactly those based on the least-squares criterion.  Not close; exactly the same.  So where the OLS methods can be used, the maximum likelihood results agree perfectly.  But where OLS isn’t feasible MLE works like a champ, providing robust parameter estimates for censored regression models.