Probabilistics 5
“Probabilistics” 5
There is more to Monte Carlo simulation than replacing constants with probability densities.
Possible Remedies (all of them wrong):
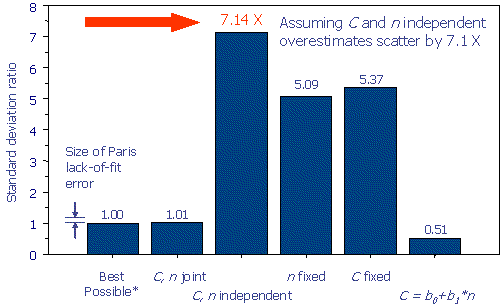
Assuming \(C\) and \(n\) to be independent, when they obviously are not (the most common error in Monte Carlo modeling), results in unacceptable error in simulated lifetime scatter. Possible remedies that have been suggested are:
- \(n\) assumed fixed, \(C\) is normal
- \(C\) assumed fixed, \(n\) is normal
- \(C\) assumed a linear function of \(n\).
Fixing either \(n\) or \(C\) seems at first blush like a reasonable solution, and it does reduce the over-prediction of scatter from 7.1X to 5.1X (\(n\) fixed) or 5.4X (\(C\) fixed). While this is an obvious improvement, the error remains wildly unacceptable. Sadly, it is at this stage when the standard deviation of \(C\) or n is arbitrarily “adjusted,” i.e. fudged until a believable result is achieved.
The Right Way:
We have considered four very common oversights in Monte Carlo modeling. So, how do you do it correctly?
Parameters estimates for \(C\) and \(n\) are jointly distributed. (Notice that this is not optional. It is how regression model parameters naturally behave. You can’t choose the ratio of a circle’s circumference to its diameter to be an integer because it might be more convenient. The fact is that \(\pi\) is inconveniently transcendental.
Similarly, regression parameter estimates are asymptotically multivariate normal, and correlated, so any realistic simulation must sample from their correlated joint density.) Modeling them as bivariate normal in a MC simulation produces a standard deviation of 0.02802 in \(\log_{10}\) integrated lifetime for 1000 samples, which is very close to the standard deviation of the integrated individual Paris fits, 0.02769. The ratio of standard deviations is 1.012. Modeling the joint behavior correctly reduces the greater than 700% error in the estimate of the standard deviation to about 1%.
These results are summarized in the following figure:
(Continued …)