Precision and Bias
Being unbiased isn’t always a good thing.
“Unbiased” is often misunderstood to mean “superior.” That is only true if an unbiased estimator has superior precision too. But biased estimators often have smaller overall error than unbiased ones. Clearly both criteria must be considered for an estimator to be judged superior to another.
The figure illustrates “bias” and “precision” and shows why bias should not be the only criterion for estimator efficacy. Would you rather have your average shot fall somewhere near the target with broad scatter, or would you trade a small offset for being close most of the time?
Bias is the average difference between the estimator and the true value. Precision is the standard deviation of the estimator. One measure of the overall variability is the Mean Squared Error, MSE, which is the average of the individual squared errors. The MSE is also the sum of the square of the precision and the square of the bias, Mean Squared Error, so the overall variability, in the same units as the parameter being estimated, is the Root Mean Squared Error, Root Mean Squared Error. Often the overall variability of a biased estimator is smaller than that for an unbiased estimator, as illustrated in the figure (upper right), in which case the biased estimator is superior to the unbiased one.
Being unbiased isn’t always a good thing if it also results in greater overall variability.
Please remember that when someone tells you he can’t use MLEs because they are “biased.” Ask him what the overall variability of his estimator is.
MLEs are “biased”
MLEs are often biased. (Not always, but sometimes.) That means that the long-run expected value of the estimator differs from the true value by some small amount called a “bias.” Often the bias can be corrected, as it is, for example, in the familiar denominator of the unbiased estimator for the standard deviation of a normal density. (That’s where that “\(n-1\)” comes from.)
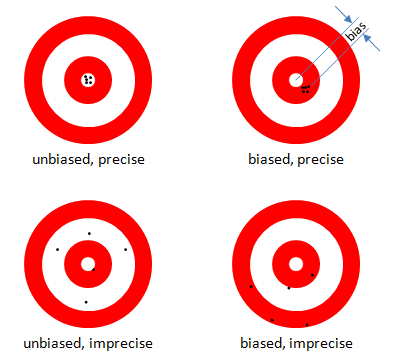
Figure 1 Being unbiased isn’t always a good thing.

