The mathematical properties of the FORM (First Order Reliability Method) have been studied extensively by engineers for more than three decades. Focus has been on the non-linearity of the limit-state function (g-function) caused by the “transformation” of variables into Normals. Even when the variables are already Normal, the non-linearity of the g-function can sometimes be troublesome, and this too has been extensively studied and remedies such as SORM (Second Order RM) have been proposed. What has not been studied, however, is the statistical, as contrasted with the mathematical, behavior of FORM.Figure 1 illustrates the FORM paradigm simplified to only two dimensions, demand and capacity. The joint distribution of demand and capacity is “transformed” into an equivalent bivariate normal density. In this study the marginal distributions were defined to be normal to simplify the problem and to illustrate that the behavior is not a result of improper “transformation.” The g-function is where demand equals capacity so that it divides the space into fail and not-fail regions depending on whether demand exceeds capacity. The b factor then is the shortest distance from the center of the joint density to the g-function, in units of standard deviations.

The FORM/SORM Paridigm

Warning: The units are rubber-band yardsticks

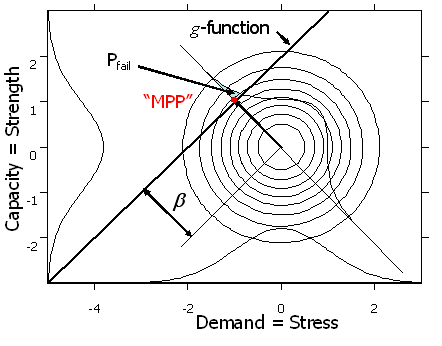
Figure 1 The Form/SORM Paradigm

NESSUS will always see the problem this way, after subtracting the sample mean and dividing by the sample standard deviation.

 This work contrasts the statistical and mathematical behavior using 10,000 nominally identical NESSUS/FORM problem evaluations, and observes that for a simple cantilever beam example the average expected number of failures is more than \(50 \times\) the nominal value. Figure 2 presents the simple cantilever beam problem.

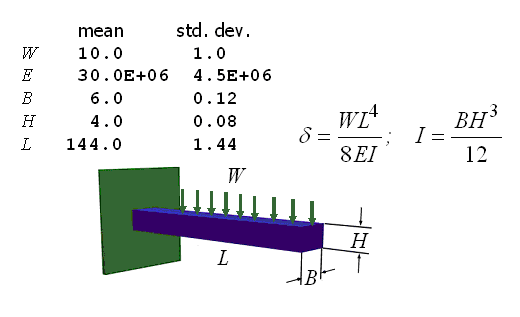
Figure 2 Cantilever Beam Example

The problem defined the nominal case as “truth,” and a NESSUS evaluation of the “known” parameter values provided the “true” result. Since in any real situation the true values would not be known, they would have to be estimated from random samples, as is stated in the NESSUS User’s Manual.

To simulate this, samples of ten were drawn from each of the five “true” marginal probability densities and the sample means and standard deviations were computed and then used in a NESSUS/FORM evaluation of the cantilever beam. The resulting “most probable point” (MPP) was recorded, and then correctly scaled by the “true” means and standard deviations and the “true” probability of failure was then determined as the normal inverse of the beta vector. This process was repeated 10,000 times.

The results demonstrate that the statistical output of FORM calculations can be very different from what might be expected mathematically, such that average probability of failure is almost always underestimated. While this result may be unexpected by practitioners for whom the terms “statistical” and “mathematical” are synonymous, it is entirely consistent with statistical theory well-known in the statistical literature for 100 years.

Next \(\Rightarrow\)