FORM-SORM and g-functions

How Reliable are First Order and Second Order Reliability Methods? (answer: scary)

Engineers who would never consider using an untested physical hypothesis (that’s why we do so much hardware testing) are sometimes guilty of using statistical methods without testing their implicit assumptions (like independence or Normality, or even randomness).

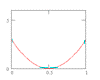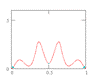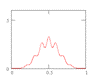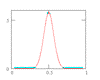
Assuming statistical independence to make the number crunching easier isn’t the only example of statistical misuse that has found its way into the contemporary probabilistic engineering literature. Among the more common statistical oversights are assuming normal behavior without verification, and using the correlation coefficient in lieu of physics. This is most often done by oversight, yet is at the heart of the limit-state function (g-function) methodology. Statistical nuance can make the difference between an answer that’s right, and one that’s dangerously wrong. But it is the ubiquitous g-function that illustrates that, with FORM/SORM, GIGO (Garbage In, Garbage Out and often, Goodness In, Garbage OUT.

I created the FORM/SORM discussion pages years ago. More recently I had the good fortune to analyze some historically famous laboratory data that illustrates that the central tenet of the FORM/SORM method – the so-called “Most Probable Point” – is a fantasy.

Here’s the plan: First we’ll review the thinking behind FORM/SORM, which admittedly seems reasonable. Unfortunately it is based on the fallacy that parameter estimates are parameter values, and they are not. They are estimates, and some really smart statisticians have tripped over the difference.