Censored Likelihood
Likelihood is “the probability of the data.”
It is proportional to the probability that the experiment turned out the way it did.
So some statistical model parameters are more likely than others because they explain the observed failures better than other values. We choose the “best” parameter values, i.e. those that maximize the likelihood, which are called, not surprisingly, “maximum likelihood parameter estimates.” We’ll use the Weibull as an example.
The most likely parameter values, given the data, for the Weibull slope, \(\beta\), and location, \(\eta\), are the “\(+\)” in Figure 1, but other values are also plausible, although less likely. That (\(\beta, \eta\)) pair produces the best fit of the data, shown as the black line in Figure 2.
The dataset below is severely right-censored: 58 of the 70 components were removed from service at various times before they failed, and are indicated by red tic-marks along the top of figure 2. 12 failed, plotted as points. The data are from Meeker and Escobar (1998), Statistical Methods for Reliability Data, Wiley, Table C-1, p630.
Note: If the figures get out of sync, please reload the page. To see an example with uncensored data, click here.
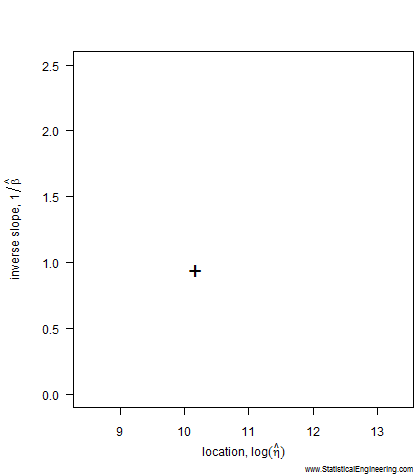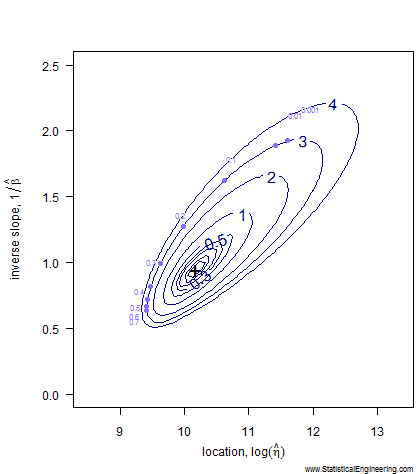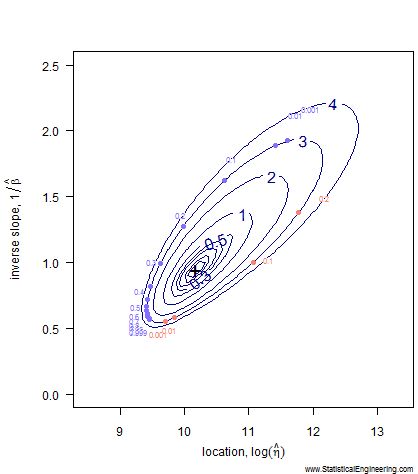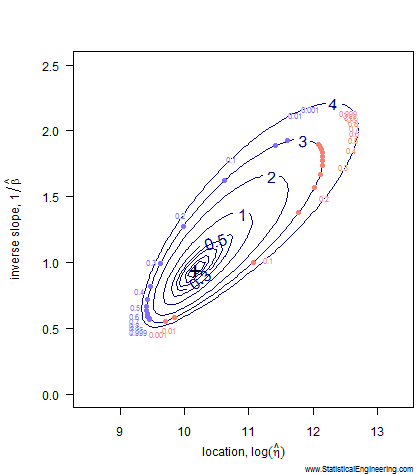 | 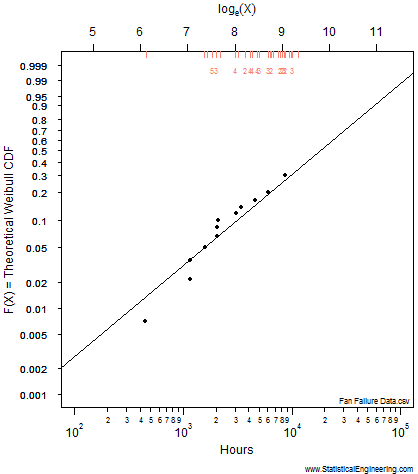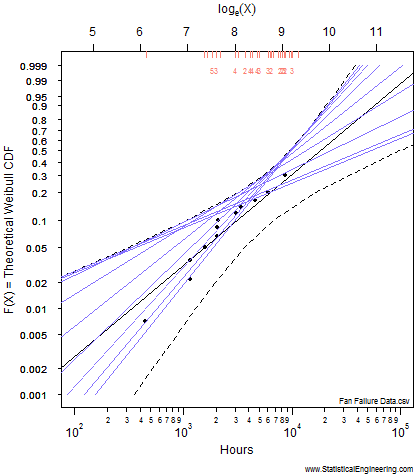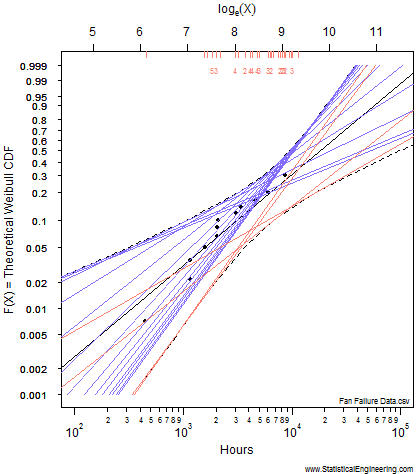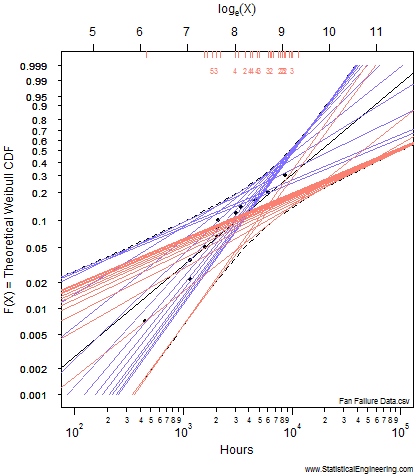 |
Figure 1 Loglikelihood Ratio Surface. Each point corresponds to a line in Figure 2. | Figure 2 Each line has a intercept and slope: a point on Figure 1. |
Notice that even after transformation the confidence “ellipse” isn’t very elliptical. It is very asymmetric along its major and minor axes, especially the major axis. That is why we choose not to use methods that employ an ellipse to approximate the loglikeihood surface (like inverting the Fisher Information Matrix) and use the true loglikelihood ratio instead.
Each point along the 95% confidence contour of the loglikelihood surface (Figure 1) produces a Weibull line (Figure 2).
The most likely parameter values, given the data, for the Weibull slope, \(\beta\), and location, \(\eta\), are the “\(+\)” but other values are also plausible, although less likely. That (\(\beta\), \(\eta\)) pair produces the best fit of the data, shown as the black line in Figure 2.